Chapitre 1 - Expressions et instructions▲
1-1. Expressions▲
Une expression est une manière de représenter un calcul. Par exemple, l'aire d'un disque de rayon r est donnée par l'expression :
kitxmlcodelatexdvp\pi r^2finkitxmlcodelatexdvpCette expression est composée de plusieurs sous-expressions. Certaines sous-expressions ne peuvent plus être décomposées, elles sont atomiques. Il s'agit soit de constantes, soit de variables, soit de fonctions ou d'opérateurs.
Dans les formules les grandeurs possèdent ce que les physiciens appellent des dimensions, en informatique on parle plutôt de types.
Lorsqu'on écrit de manière traditionnelle une expression, un certain nombre de conventions d'écriture nous permet d'omettre certains signes d'opérations. Ici, par exemple, les signes de multiplications sont implicites. Lorsqu'on souhaite traduire cette expression de manière informatique, il faudra savoir que des règles strictes devront être appliquées, l'ensemble de ces règles forme la syntaxe du langage, et il faudra absolument les respecter pour espérer obtenir un résultat.
1-2. Le logiciel Objective Caml▲
Le langage informatique que nous utiliserons pour ce cours est Caml. On peut utiliser ce langage dans différents modes.
- En mode interprété : dans ce mode le programmeur dialogue (en Caml) avec un interprète du langage. Plus précisément, il rédige des phrases qu'il communique à l'interprète, et celui-ci vérifie qu'elles sont bien rédigées et donne en retour une réponse au programmeur. Le mode interprété permet au programmeur d'évaluer immédiatement et pas à pas ses idées.
- En mode compilé : dans ce mode, le programmeur rédige (avec un éditeur de texte) l'intégralité de son programme, puis le soumet à un compilateur du langage dont le rôle est de produire un programme exécutable. Si le programme est correctement rédigé (aucune erreur de syntaxe, cohérence des types dans les expressions…), il ne reste plus au programmeur qu'à lancer l'exécution de son programme et vérifier la conformité de cette exécution au cahier des charges initial.
Dans ce cours, nous n'utiliserons que le mode interprété. La compilation sera abordée dans un autre cours.
Caml est un langage développé par l'INRIA (Institut National de Recherche en Informatique et Automatique) que l'on peut télécharger à l'adresse http://caml.inria.fr/. On en trouve différentes implantations et celle que nous utiliserons est Objective Caml. Objective Caml est un logiciel libre qui peut être téléchargé depuis l'adresse précédente ainsi que le manuel d'utilisation(3). Il en existe des versions pour les plateformes les plus courantes : Linux, Microsoft Windows, MacOS X. Dans ce polycopié, ainsi que dans les salles de TP, nous utiliserons une version pour Linux.
Pour débuter une session de dialogue avec l'interprète d'Objective Caml, on tape la commande ocaml dans un terminal.
2.
3.
> ocaml
Objective Caml version 3.10.2
#
Le symbole dièse (#) est l'invite de l'interprète : c'est le signe qu'il est prêt à vous écouter et à exécuter la commande que vous lui donnerez.
Avant de découvrir les premières expressions et instructions du langage Caml, voyons celle qui permet de quitter l'interprète. C'est la directive(4) #quit.
2.
# #quit ;;
>
1-3. Premières expressions en Caml▲
1-3-1. Expressions numériques▲
La syntaxe des expressions numériques est très proche de la notation mathématique usuelle. Ci-dessous, l'expression en Caml pour l'expression
kitxmlcodelatexdvp\frac{4 \times (-3+5)}{2}\qquad(1,1)finkitxmlcodelatexdvpaccompagnée de la réponse fournie par l'interprète.
2.
# (4 * (-3 + 5)) / 2 ;;
- : int = 4
Analysons ce point de dialogue avec l'interprète.
- Tout d'abord l'expression (
4*(-3+5))/2. Elle est très proche de la notation mathématique usuelle, les nombres sont notés comme d'habitude, l'addition et la division aussi, la multiplication est notée*, et on utilise des parenthèses pour marquer ici la priorité de certaines opérations sur d'autres. - L'expression est terminée par un double point-virgule (;;). C'est une situation générale dans tout dialogue avec l'interprète, le double point-virgule marque la fin d'une phrase que l'on souhaite communiquer à l'évaluation. Ce marqueur mis, il ne reste plus qu'à le faire suivre d'un « retour-chariot » (touche Entrée du clavier) pour soumettre la phrase à l'interprète.
- Si l'expression ne contient aucune erreur de syntaxe, et est typable(5), alors l'interprète procède à son évaluation et en donne le résultat. Dans le cas présent, l'expression est parfaitement bien formée (aucune erreur de syntaxe), elle est correcte du point de vue des types mis en jeux, et l'interprète nous indique que cette expression a une valeur de type numérique entier (int) et que sa valeur est l'entier 4.
Précisons tout de suite qu'une expression ne doit pas nécessairement être écrite sur une seule ligne. On peut écrire une expression sur autant de lignes que l'on veut. C'est le marqueur de fin ;; qui indique à l'interprète que la rédaction de l'expression est achevée. Voici la même expression rédigée sur plusieurs lignes.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
# (
4
*
(
-3
+
5
)
)
/
2
;;
- : int = 4
L'opération de division sur les nombres entiers fournit le quotient dans la division euclidienne.
Par exemple 7/3 vaut 2 et non pas environ 2.3333. Le reste de la division est obtenu avec l'opérateur mod.
2.
3.
4.
5.
6.
# 7 / 3 ;;
- : int = 2
# 7 mod 3 ;;
- : int = 1
# 3 * 2 + 1 ;;
- : int = 7
Bien entendu, on peut calculer des nombres non entiers que nous nommerons nombres flottants ou simplement flottants(6). En Caml, ces nombres sont tous marqués d'un séparateur décimal, le point, qu'ils soient ou non dotés de chiffres après la virgule.
2.
3.
4.
# 2. ;;
- : float = 2.
# 2.333 ;;
- : float = 2.333
Comme on peut le voir sur ces deux exemples, le type de ces nombres est float, pour nombre à « virgule flottante ».
En Caml, il faut distinguer les opérateurs arithmétiques portant sur des nombres entiers, de ceux portant sur des nombres non entiers. Les opérateurs pour les quatre opérations usuelles (addition, soustraction, multiplication et division) portant sur les nombres de type float sont identiques à ceux portant sur les nombres entiers, mais suivis d'un point. Voici l'expression arithmétique (1.1) ci-dessus, évaluée avec des nombres de type float.
2.
# (4. *. (-. 3. +. 5.)) /. 2. ;;
- : float = 4.
Caml refuse systématiquement toute expression numérique où sont mélangés des nombres de natures différentes.
2.
3.
4.
# 1 + 2. ;;
This expression has type float but is here used with type int
# 1 +. 2. ;;
This expression has type int but is here used with type float
Les deux fonctions int_of_float et float_of_int assurent la conversion d'un nombre d'un type à l'autre.
2.
3.
4.
5.
6.
7.
8.
9.
10.
# int_of_float (-2.7) ;;
- : int = -2
# int_of_float (2.7) ;;
- : int = 2
# float_of_int (2);;
- : float = 2.
# 1 + int_of_float (2.) ;;
- : int = 3
# 1. +. float_of_int (2) ;;
- : float = 3.
Il existe de très nombreuses autres fonctions. En voici quelques-unes :
- sur les entiers : abs (valeur absolue d'un nombre entier) ;
- sur les non entiers : abs_float (valeur absolue d'un flottant), sqrt (racine carrée d'un flottant), exp (exponentielle de base e), log (logarithme népérien), cos, sin, tan, et bien d'autres encore.
1-3-2. Expressions booléennes▲
En programmation, les expressions booléennes sont nécessaires pour effectuer des calculs ou exécuter des instructions dépendant de la réalisation ou non de certaines conditions (cf chapitres 2Chapitre 2 - Conditions, expressions et instructions conditionnelles et 3Chapitre 3 - Instructions conditionnellement répétées).
Les booléens forment un ensemble à deux valeurs seulement, désignés en Caml par true (vrai) et false (faux). Le type des booléens est désigné par bool.
Les expressions booléennes sont les expressions qui ont pour valeur l'un des deux booléens. Elles apparaissent naturellement dans les comparaisons.
2.
3.
4.
5.
6.
7.
8.
9.
10.
# true ;;
- : bool = true
# false ;;
- : bool = false
# 1 = 5-4 ;;
- : bool = true
# 1 < 5-4 ;;
- : bool = false
# 1 >= 5-4 ;;
- : bool = true
Les opérateurs logiques usuels sont && (et), || (ou) et not (négation).
2.
3.
4.
5.
6.
# (1 = 1) && (1 = 0) ;;
- : bool = false
# (1 = 1) || (1 = 0) ;;
- : bool = true
# not (1 = 0) ;;
- : bool = true
Le chapitre 2Chapitre 2 - Conditions, expressions et instructions conditionnelles donne plus de précisions sur les opérateurs logiques et les expressions booléennes, ainsi que sur les expressions et instructions booléennes.
1-3-3. Caractères et chaînes de caractères▲
Les caractères forment un type nommé char en Caml qui comprend 256 valeurs. Parmi ces valeurs on trouve toutes les lettres de l'alphabet latin dans leur version minuscule et majuscule, ainsi que les dix chiffres, et des symboles de ponctuation.
Une expression littérale de type char est obtenue en plaçant le caractère voulu entre apostrophes.
2.
3.
4.
5.
6.
7.
8.
# 'A';;
- : char = 'A'
# 'a';;
- : char = 'a'
# '1';;
- : char = '1'
# '?';;
- : char = '?'
Les chaînes de caractères sont des suites finies de caractères placés les uns à la suite des autres. Elles peuvent ne contenir aucun caractère : chaîne vide, et elles peuvent en contenir jusqu'à 224 - 6, soit plus de 16 millions de caractères. En Caml, elles sont mises entre guillemets et leur type est désigné par string.
2.
3.
4.
# "Aa1?" ;;
- : string = "Aa1?"
# "";;
- : string = ""
L'opérateur de concaténation qui construit une chaîne en mettant bout à bout deux chaînes est désigné par ^.
2.
# "InitProg"^" c'est vachement bien !";;
- : string = "InitProg c'est vachement bien !"
Le chapitre 7Chapitre 7 - Caractères et chaînes de caractères est consacré à une présentation plus détaillée des caractères et chaînes de caractères.
1-4. Instructions▲
En Caml, une instruction est une expression dont la valeur est de type unit(7). Ce type ne contient qu'une seule valeur notée (). Par conséquent, cela signifie que toute instruction a pour valeur (), que cette valeur est connue avant même que l'expression ne soit évaluée, et donc que ce qui importe n'est pas tant la valeur de l'instruction, que l'effet de bord qu'elle produit. Et d'ailleurs, plutôt que de parler d'évaluation de l'expression, on dit plutôt exécution de l'instruction.
Les effets de bord produits par l'exécution d'une instruction peuvent être de plusieurs natures :
- modification de la valeur de l'environnement courant de travail, par exemple en modifiant la valeur d'une variable mutable (cf chapitre 4Chapitre 4 - Constantes, variables) ;
- communication du programme avec le monde extérieur, par exemple, par lecture ou écriture d'une valeur.
Voici la plus simple (et la plus inutile) des instructions.
2.
# () ;;
- : unit = ()
L'exécution de cette instruction ne provoque aucun effet de bord (ni modification de variable, ni lecture, ni écriture). Seule sa valeur est fournie par l'interprète.
1-4-1. Instructions d'impression▲
Plus intéressantes sont les instructions pour imprimer ou écrire des valeurs. Elles se distinguent selon le type des valeurs à imprimer. En voici quatre illustrées chacune par un exemple.
2.
3.
4.
5.
6.
7.
8.
# print_int (8) ;;
8- : unit = ()
# print_float (8.) ;;
8.- : unit = ()
# print_string ("8") ;;
8- : unit = ()
# print_char ('8') ;;
8- : unit = ()
Il faut bien comprendre la réponse de l'interprète à l'exécution de ces instructions d'impression. Dans chacun des cas, on peut voir l'impression de la valeur donnée à ces instructions, immédiatement suivie par la valeur de l'instruction qui est immuablement - : unit = ().
On pourrait préférer qu'un saut de ligne distingue la valeur imprimée de la valeur de l'instruction. La fonction print_endline effectue un saut de ligne immédiatement après avoir imprimé ce qu'on lui demande. Mais cette fonction ne permet l'impression que des chaînes de caractères.
2.
3.
# print_endline ("Timoleon apprend a programmer en Caml") ;;
Timoleon apprend a programmer en Caml
- : unit = ()
Une autre instruction provoque des sauts de ligne : l'instruction print_newline ().
2.
# print_newline () ;;
- : unit = ()
Comme on peut le voir sur cet exemple, cette instruction ne prend aucun paramètre. Elle se contente d'imprimer un saut de ligne, et si rien auparavant n'a été imprimé, comme c'est le cas ici, on obtient une ligne vide. Cette instruction suit en général d'autres instructions d'impression, et nécessite d'exécuter une séquence d'instructions. Cette notion de séquence d'instructions est présentée dans la section 1.4.3Séquence d'instructions.
1-4-2. Instructions du module Cartes▲
Le module Cartes est une extension du langage Caml qui permet de manipuler des tas de cartes à jouer. Ce module est présenté dans l'annexe AAnnexe A - Les cartes.
Deux instructions y sont définies :
- L'instruction init_tas(n,s) qui initialise le tas numéro n avec une pile de cartes décrite par la chaîne de caractères s ;
- Et l'instruction deplacer_sommet(n,p) qui déplace une carte du tas numéro n vers le tas numéro p.
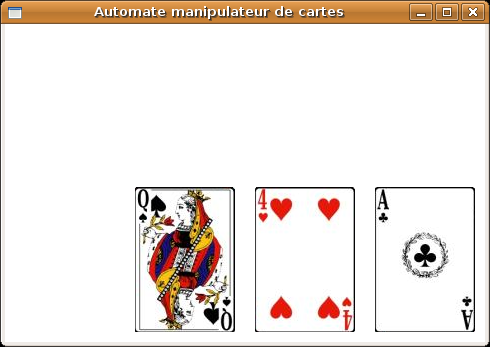
Par exemple, en supposant qu'initialement aucun tas ne contienne de cartes, alors le dialogue(8) qui suit donne le tas tel qu'on peut le voir sur la figure 1.1.
2.
# init_tas (1,"TCP") ;;
- : unit = ()
Comme on peut le constater sur la figure 1.1, l'effet de bord provoqué par cette instruction est une initialisation du tas numéro 1 avec trois cartes de couleurs successives ♣, ♡ et ♠.
En poursuivant le dialogue avec l'interprète, on déplace la carte au sommet du tas numéro 1 vers le tas numéro 2 et la situation atteinte est celle montrée sur la figure 1.2.
2.
# deplacer_sommet (1,2) ;;
- : unit = ()
L'effet de bord de l'instruction deplacer_sommet (1,2) est la transformation de l'état des cartes.
1-4-3. Séquence d'instructions▲
Supposons qu'initialement seul le premier tas de cartes n'est pas vide, et que ce tas contient trois cartes de couleur ♣, ♡, ♠ dans cet ordre de bas en haut (cf figure 1.1). Supposons que nous voulions vider le tas 1 en plaçant une carte sur chacun des trois autres tas (cf figure 1.3).
Cela peut se faire simplement en déplaçant une à une les cartes du tas 1 vers les autres tas comme le montre l'algorithme 1.1.
|
Algorithme 1.1 Mettre les trois cartes du tas 1 vers les tas 2, 3 et 4 |
|
1: déplacer le sommet du tas 1 vers le tas 2 |
En Caml, cet algorithme se traduit simplement par trois instructions deplacer_sommet.
Si on utilise la boucle de dialogue avec l'interprète du langage, on atteint la situation voulue avec le dialogue :
2.
3.
4.
5.
6.
# deplacer_sommet(1,2);;
- : unit = ()
# deplacer_sommet(1,3);;
- : unit = ()
# deplacer_sommet(1,4);;
- : unit = ()
Dans ce dialogue, chacune des trois instructions est donnée à exécuter les unes après les autres, et l'interprète donne le résultat de son travail après chacune d'elles (la mention - : unit = ()).
On peut aussi regrouper ces trois instructions en une seule :
2.
3.
4.
# deplacer_sommet(1,2);
deplacer_sommet(1,3);
deplacer_sommet(1,4);;
- : unit = ()
L'usage du simple point-virgule pour séparer les instructions permet de les transmettre à l'interprète en une seule fois, et celui-ci ne donne qu'une seule réponse. En un seul ordre, nous avons commandé l'exécution de trois instructions.
Cette construction est très fréquente en programmation impérative, et on la nomme séquence d'instructions. En Caml, une séquence d'instructions s'obtient en séparant les instructions par un simple point-virgule. Dans une séquence d'instructions, le nombre d'instructions n'est pas limité.
2.
3.
4.
< instruction 1 >;
< instruction 2 >;
…
< instruction n >
Lorsqu'une séquence d'instructions est exécutée, toutes les instructions qui la composent sont exécutées les unes après les autres dans l'ordre de leur apparition dans la séquence. La valeur fournie d'une séquence est la valeur de la dernière instruction, c'est-à-dire () en général.
Voici un autre exemple d'utilisation de la séquence d'instructions pour produire un affichage d'une ligne composée de plusieurs éléments de types distincts.
2.
3.
4.
5.
# print_string ("(4 * (-3 + 5)) / 2 = ");
print_int ((4 * (-3 + 5)) / 2) ;
print_newline () ;;
(4 * (-3 + 5)) / 2 = 4
- : unit = ()
On verra qu'il est parfois nécessaire de parenthéser(9) une séquence d'instructions pour éviter certaines ambiguïtés (cf chapitre 2.5.1Remarque sur le parenthésage). En Caml cela peut se faire avec des parenthèses ouvrantes et fermantes, ou bien avec les deux mots-clés du langage begin et end. Dans la suite nous désignerons par bloc d'instructions toute séquence placée entre ces deux mots.
2.
3.
begin
(* sequence d'instructions *)
end
Ce parenthésage n'a que pour seule vocation à éviter des ambiguïtés syntaxiques, et ne change rien à l'exécution de la séquence qu'il contient.
2.
3.
4.
5.
6.
7.
# begin
print_string ("(4 * (-3 + 5)) / 2 = ");
print_int ((4 * (-3 + 5)) / 2) ;
print_newline ()
end ;;
(4 * (-3 + 5)) / 2 = 4
- : unit = ()
1-5. Exercices▲
1-5-1. Expressions numériques▲
Exercice 1-1
Évaluations d'expressions arithmétiques
Pour chacune des expressions arithmétiques qui suivent, évaluez-les avec Objective Caml en arithmétique sur les entiers (int) et en arithmétique sur les flottants (float).
- kitxmlcodeinlinelatexdvp(3 + 4) \times 5finkitxmlcodeinlinelatexdvp.
- kitxmlcodeinlinelatexdvp3 + (4 \times 5)finkitxmlcodeinlinelatexdvp.
- kitxmlcodeinlinelatexdvp3 + 4 \times 5finkitxmlcodeinlinelatexdvp.
- kitxmlcodeinlinelatexdvp125 \times (12 - \frac{204}{6})finkitxmlcodeinlinelatexdvp.
- kitxmlcodeinlinelatexdvp125 \times (12 - \frac{204}{5})finkitxmlcodeinlinelatexdvp.
Pour la dernière expression, expliquez la différence sensible entre la valeur obtenue en arithmétique entière, et celle en arithmétique flottante.
1-5-2. Instructions▲
Exercice 1-2
Impressions de valeurs
Question 1 Utilisez l'une des instructions print_… pour imprimer la valeur des expressions de l'exercice
Question 2 Écrivez une instruction qui imprime une expression arithmétique, puis le signe =, puis la valeur de l'expression arithmétique et enfin un passage à la ligne. Voici un exemple, dans lequel l'instruction a été effacée.
2.
3.
# (* instruction effacee *)
(3+4) *5 = 35
- : unit = ()
Trouvez une séquence d'instructions qui réalise cela, puis cherchez une seule instruction.