Chapitre 2 - Conditions, expressions et instructions conditionnelles▲
Le problème▲
État initial : tas 1 un trèfle ou un pique, les autres tas sont vides.
État final : tas 1 et 4 vides, le tas 2 contient le trèfle ou rien et le tas 3 contient le pique ou rien.
Algorithme▲
La résolution du problème nécessite une étude de cas :
|
Algorithme 2.1 Solution du problème |
|
si la carte au sommet du tas 1 est un trèfle alors |
Expressions booléennes▲
Booléens▲
On appelle booléen(10) l'une des deux valeurs de vérité vrai ou faux. On désigne en abrégé ces deux valeurs par les deux lettres V et F.
Une expression booléenne est une expression qui prend une valeur booléenne, autrement dit l'une ou l'autre des deux valeurs V ou F.
Les expressions booléennes servent à exprimer des conditions. Elles peuvent être :
- simples ;
- ou composées.
Expressions simples▲
Les expressions booléennes simples sont de la forme : « la carte au sommet du tas 1 est un trèfle »
Expressions composées▲
L'opérateur ou
L'expression E = « la carte au sommet du tas 1 est un trèfle ou un carreau » peut se décomposer en deux expressions simples :
- E1 = « la carte au sommet du tas 1 est un trèfle » ;
- E2 = « la carte au sommet du tas 1 est un carreau »,
Le lien les unissant étant le connecteur ou opérateur logique ou
|
E = E1 ou E2 |
L'expression E est donc composée.
L'expression E ne prend la valeur V que si au moins l'une des deux expressions E1, E2 est vraie.
On résume cette définition de l'opérateur ou par la table de vérité représentée par le tableau 2.1
|
E1 |
E2 |
E1 ou E2 |
|---|---|---|
|
V |
V |
V |
|
V |
F |
V |
|
F |
V |
V |
|
F |
F |
F |
L'opérateur et
L'expression E = « la carte au sommet du tas 1 est un trèfle et sa valeur est supérieure à celle de la carte située au sommet du tas 2 » peut se décomposer en deux expressions simples :
- E1 = « la carte au sommet du tas 1 est un trèfle » ;
- E2 = « la carte au sommet du tas 1 a une valeur supérieure ou égale à celle du tas 2 »,
Le lien les unissant étant le connecteur ou opérateur logique et
|
E = E1 et E2 |
L'expression E est donc composée.
L'expression E ne prend la valeur V que si les deux expressions E1, E2 sont vraies.
On résume cette définition de l'opérateur et par la table de vérité représentée par le tableau 2.2.
|
E1 |
E2 |
E1 et E2 |
|---|---|---|
|
V |
V |
V |
|
V |
F |
F |
|
F |
V |
F |
|
F |
F |
F |
L'opérateur non
L'expression E = « la carte au sommet du tas 1 n'est pas un trèfle » peut se décomposer en une expression plus simple :
- E1 = « la carte au sommet du tas 1 est un trèfle »,
que l'on nie.
|
E = non(E1) |
L'expression E est donc composée.
La valeur de l'expression E est opposée à celle de E1.
On résume cette définition de l'opérateur non par la table de vérité représentée par le tableau 2.3.
|
E1 |
non(E1) |
|---|---|
|
V |
F |
|
F |
V |
Propriétés des opérateurs▲
a, b et c sont trois expressions booléennes.
|
Double négation |
non(non(a)) = a |
|
Élément neutre du ou |
a ou F = a |
|
Élément neutre du et |
a et V = a |
|
Élément absorbant du ou |
a ou V = V |
|
Élément absorbant du et |
a et F = F |
|
Idempotence du ou |
a ou a = a |
|
Idempotence du et |
a et a = a |
|
Tautologie |
a ou non(a) = V |
|
Contradiction |
a et non(a) = F |
|
Commutativité du ou |
a ou b = b ou a |
|
Commutativité du et |
a et b = b et a |
|
Associativité du ou |
(a ou b) ou c = a ou (b ou c) |
|
Associativité du et |
(a et b) et c = a et (b et c) |
|
Distributivité du et par rapport au ou |
a et (b ou c) = (a et b) ou (a et c) |
|
Distributivité du ou par rapport au et |
a ou (b et c) = (a ou b) et (a ou c) |
|
Loi de Morgan (1) |
non(a ou b) = non(a) et non(b) |
|
Loi de Morgan (2) |
non(a et b) = non(a) ou non(b) |
En Caml▲
Booléens▲
En Caml, les deux valeurs booléennes définissent le type bool.
|
vrai |
|
|
faux |
|
Expressions booléennes▲
Les expressions booléennes simples peuvent s'exprimer en Caml par :
- des valeurs littérales
trueoufalse; - une variable booléenne (voir plus tard) ;
- une expression décrivant une relation ;
- un appel à une fonction à valeurs booléennes.
Exemple 1 :
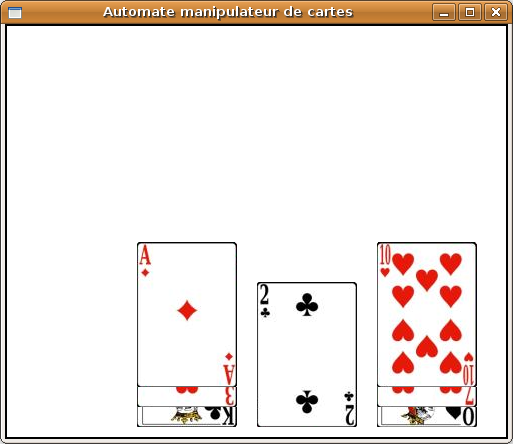
Tous les exemples donnés par la suite s'appuient sur une configuration des tas donnée à la figure 2.1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
# true ;;
- : bool = true
# false ;;
- : bool = false
# tas_vide(1);;
- : bool = true
# tas_non_vide(1);;
- : bool = false
# couleur_sommet(2) = PIQUE;;
- : bool = false
# couleur_sommet(2) = CARREAU;;
- : bool = true
# sommet_trefle(3);;
- : bool = true
Les expressions composées se traduisent avec les opérateurs logiques &&, || et not.
|
Opérateur logique |
et |
ou |
non |
|
En Caml |
&& |
|| |
|
Exemple 2 :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
# true && true;;
- : bool = true
# true && false;;
- : bool = false
# true || false;;
- : bool = true
# false || false;;
- : bool = false
# not (true);;
- : bool = false
# not (false);;
- : bool = true
# sommet_carreau(2) && sommet_trefle(3) ;;
- : bool = true
# sommet_carreau(2) && not (sommet_coeur(3)) ;;
- : bool = true
# tas_non_vide(1) || sommet_coeur(4);;
- : bool = true
Attention :▲
Les opérateurs && et || n'agissent que sur des booléens !
On pourrait être tenté, pour exprimer que la carte au sommet du tas 1 soit un trèfle ou un carreau, d'écrire
couleur_sommet(1) = TREFLE || CARREAU
mais cela est incorrect car TREFLE et CARREAU ne sont pas des booléens, mais des couleurs. Il faut donc écrire
couleur_sommet(1) = TREFLE || couleur_sommet(1) = CARREAU
même si cela semble bien lourd.
Remarque sur les opérateurs && et ||▲
En logique booléenne, les opérateurs et et ou sont commutatifs
|
a et b = b et a |
En Caml, ces opérateurs ne sont pas commutatifs : les arguments sont évalués séquentiellement de gauche à droite.
Exemple 3 :
En Caml, les expressions tas_non_vide(1) && sommet_trefle(1) et sommet_trefle(1) && tas_non_vide(1) ne sont pas équivalentes :
- l'évaluation de la première expression ne déclenche jamais d'exception, car si le tas 1 est vide, sommet_trefle(
1) n'est pas évalué, puisque la valeur de l'expression complète est alors déterminée ;
2.
# tas_non_vide(1) && sommet_trefle(1);;
- : bool = false
- en revanche l'évaluation de la seconde expression déclenche une exception si le tas 1 est vide.
2.
# sommet_trefle(1) && tas_non_vide(1) ;;
Exception: LesExceptions.Tas_Vide 1.
Expressions conditionnelles▲
Les expressions conditionnelles sont des expressions qui déterminent l'expression à évaluer en fonction de la validité d'une condition.
2.
3.
4.
if < condition > then
< expression 1 >
else
< expression 2 >
Exemple 4 :
Dans le contexte indiqué par la figure 2.1, on a
2.
3.
4.
5.
6.
7.
8.
9.
10.
# if sommet_carreau(2) then
0
else
1 ;;
- : int = 0
# if sommet_trefle(2) then
0
else
1 ;;
- : int = 1
Instructions conditionnelles▲
Les instructions conditionnelles sont des expressions conditionnelles dont la valeur est du type unit. On les utilise pour agir en fonction d'un contexte.
Instruction conditionnelle complète
L'instruction conditionnelle complète (ou alternative) permet de mener une action si une condition est satisfaite, et une autre dans le cas contraire.
2.
3.
4.
if < condition > then
(* bloc d'instructions *)
else
(* bloc d'instructions *)
Exemple 5 :
Traduction en Caml de l'algorithme décrit à la section 2.1.1Algorithme.
2.
3.
4.
5.
if sommet_trefle(1) then begin
deplacer_sommet(1,2)
end else begin
deplacer_sommet(1,3)
end
La condition est ici exprimée par l'expression booléenne (simple) sommet_trefle(1), le premier bloc d'instructions (celui qui suit le mot réservé then) est
2.
3.
begin
deplacer_sommet(1,2)
end
et le second bloc (qui suit le mot réservé else).
2.
3.
begin
deplacer_sommet(1,3)
end
Notez qu'il n'y a pas de ; après le end qui précède le else. En revanche, si cette instruction conditionnelle est suivie d'une autre, il faudra ajouter un ; après le end du second bloc (end {if};).
Instruction conditionnelle simple
Il arrive qu'une action ait besoin d'être menée si une condition est satisfaite, mais qu'aucune ne soit nécessaire sinon. C'est alors une instruction conditionnelle simple. En Caml, elle s'écrit sans la partie else.
2.
if < condition > then
(* bloc d'instructions *)
Exemple 6 :
Déplacer la carte située au sommet du tas 1 si c'est un trèfle sinon ne rien faire.
2.
3.
if sommet_trefle(1) then begin
deplacer_sommet(1,2)
end
Remarque sur le parenthésage▲
La syntaxe donnée ci-dessus pour l'instruction conditionnelle mentionne qu'après le then et le else doivent figurer des blocs d'instructions, c'est-à-dire des séquences parenthésées par begin et end.
En réalité, il n'est pas nécessaire de mettre le parenthésage lorsque la séquence ne comprend qu'une seule instruction (comme pour les expressions conditionnelles). Ainsi on peut écrire
2.
3.
4.
if sommet_trefle(1) then
deplacer_sommet(1,2)
else
deplacer_sommet(1,3)
En revanche, dès que la séquence comprend plusieurs instructions, le parenthésage devient nécessaire dans la partie else pour une instruction conditionnelle complète, et dans la partie then pour une instruction conditionnelle simple.
En effet, l'instruction
2.
3.
4.
if sommet_trefle(1) then begin
deplacer_sommet(1,2);
deplacer_sommet(2,3)
end
ne peut pas être remplacée par
2.
3.
if sommet_trefle(1) then
deplacer_sommet(1,2);
deplacer_sommet(2,3)
qui est une séquence de deux instructions :
- Une instruction conditionnelle simple ;
- Suivie d'une instruction de déplacement non soumise à condition.
Méthodologie▲
Voici quelques principes méthodologiques concernant la conception d'instructions conditionnelles :
-
Étude des cas intervenant dans le problème :
- commencer par distinguer les différents cas ;
- vérifier que ces cas sont bien exhaustifs (on n'oublie aucune situation) ;
- vérifier que ces cas ne sont pas redondants (cas exclusifs) ;
- donner un exemple de comportement attendu de l'instruction pour chacun des cas.
-
Pour chacun des cas :
- établir un test (expression booléenne) permettant de distinguer le cas ;
- déterminer la séquence d'instructions à exécuter dans ce cas.
- Construire un jeu de tests qui permet de s'assurer de la validité du programme : ce jeu doit comprendre au moins un test pour chacun des cas envisagés.
Exemple
Considérons une situation initiale où les tas numérotés de 1 à 3 contiennent un nombre quelconque non nul de cartes, et le tas 4 est vide.
2.
3.
4.
init_tas(1,"(T+K+C+P)[T+K+C+P]");
init_tas(2,"(T+K+C+P)[T+K+C+P]");
init_tas(3,"(T+K+C+P)[T+K+C+P]");
init_tas(4,"");
L'objectif à atteindre est de déplacer la carte de plus grande valeur au sommet d'un des trois tas vers le tas 4.
Résoudre ce problème revient à repérer quel tas possède en son sommet la carte de plus grande valeur.
Étude des cas
Il y a évidemment trois possibilités : c'est le tas 1 ou le tas 2 ou le tas 3. Comment les distinguer ?
- c'est le tas 1, si la carte au sommet du tas 1 est supérieure ou égale à celle du tas 2, et est supérieure ou égale à celle du tas 3 ;
- c'est le tas 2, si la carte au sommet du tas 2 est supérieure ou égale à celle du tas 1, et est supérieure ou égale à celle du tas 3 ;
- c'est le tas 3, si la carte au sommet du tas 3 est supérieure ou égale à celle du tas 1, et est supérieure ou égale à celle du tas 2.
Autrement dit c'est le tas i si la condition superieur(i,j) && superieur(i,k) (dans laquelle j et k désignent les deux numéros de tas autres que i) est satisfaite. Les conditions distinguant les trois cas ne sont pas exclusives (pensez aux cas d'égalité).
Exercices▲
Exercice 2-1
En utilisant les tables de vérité, prouvez quelques propriétés des opérateurs logiques et, ou et non.
Exercice 2-2 Ou exclusif
Si a et b sont deux expressions booléennes, le ou-exclusif de ces deux expressions, noté a⊕b, est une nouvelle expression booléenne qui est vraie si et seulement si une seule des deux expressions a ou b est vraie. La table de vérité du ou-exclusif est donnée
|
a |
b |
a ⊕ b |
|---|---|---|
|
V |
V |
F |
|
V |
F |
V |
|
F |
V |
V |
|
F |
F |
F |
Écrivez l'expression a ⊕ b à l'aide des opérateurs et, ou et non.
Exercice 2-3
Question 1 : Exprimez le fait que [a,b] et [c,d] sont des intervalles disjoints, attention au cas des intervalles vides, par exemple si a = 15 et b = -5.
Question 2 : Exprimez le fait que [a,b] et [c,d] sont des intervalles qui se recouvrent partiellement de deux manières :
- en utilisant la solution de la question précédente (c'est très simple) ;
- directement (c'est compliqué !).
Exercice 2-4 Égalité et valeur booléenne
Question 1 : Soit a une expression booléenne. Réalisez la table de vérité des expressions :
- a = V ;
- a = F.
Exercice 2-5
Question 1
Écrivez l'instruction ci-dessous sans utiliser l'opérateur non ni d'opérateurs de comparaison.
si non a alors
instr1
sinon
instr2
fin si
Question 2
Écrivez l'instruction ci-dessous sans utiliser l'opérateur et
si a et b alors
instr1
fin si
Question 3
Écrivez l'instruction ci-dessous sans utiliser l'opérateur ou
si a ou b alors
instr1
fin si
Exercice 2-6
Expliquez pourquoi le programme
2.
3.
4.
5.
6.
7.
8.
9.
if superieur(1,2) && superieur(1,3) then begin
deplacer_sommet(1,4)
end;
if superieur(2,1) && superieur(2,3) then begin
deplacer_sommet(2,4)
end;
if superieur(3,1) && superieur(3,2) then begin
deplacer_sommet(3,4)
end ;;
n'est pas correct pour le problème posé dans la section 2.6Méthodologie.
Exercice 2-7
Reprenez le problème de la section 2.6Méthodologie en admettant qu'un ou plusieurs des trois premiers tas peut être vide. Si les trois tas sont vides, on ne déplace aucune carte.