Cours complet d’initiation à la programmation

Spécifier une fonction, c'est :

• choisir un identificateur pour la nommer ;
• préciser le nombre et le type de ses paramètres, et les nommer ;
• indiquer les conditions d'utilisation (CU) que doivent vérifier les paramètres lors d'un appel à la fonction ;
• indiquer le type de la valeur qu'elle renvoie ;
• et indiquer quelle est la relation entre la valeur renvoyée et les paramètres qui lui sont passés.

Exemple 1 :

La fonction prédéfinie donnant la négation d'un booléen en Caml est une fonction nommée not, qui opère sur un paramètre de type bool, dont la valeur renvoyée est aussi de type bool et pour laquelle il n'y a aucune contrainte d'utilisation. Nous résumons tout cela par la notation :

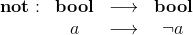
Exemple 2 :

Un autre exemple est la fonction du module Cartes qui permet de comparer les hauteurs des cartes situées au sommet de deux tas. Cette fonction est nommée superieur, elle prend deux paramètres de type Cartes.numero_tas, et renvoie une valeur de type bool. Elle possède aussi une contrainte d'utilisation qui exige qu'aucun des deux tas passés en paramètre ne soit vide. Tout cela est résumé par la notation :

Contrairement à d'autres langages tels que C, Ada ou Pascal, en Caml il n'est pas nécessaire d'apprendre de nouvelle forme syntaxique pour déclarer une nouvelle fonction. On utilise la même forme let que pour la déclaration des variables.

let <nom> (<liste parametres>) =
  (* expression simple ou sequence d'instructions
     definissant la fonction *)

Exemple 3 :

Soit à écrire le prédicat rouge dont la spécification est

Le code en Caml pour cette fonction s'écrit tout simplement

let rouge(n) =
  sommet_coeur(n) || sommet_carreau(n)

Comme on peut le constater, en Caml il n'est pas nécessaire au programmeur de préciser le type des paramètres et celui de la valeur renvoyée, contrairement au cas de langages comme C, Ada ou Pascal. C'est le langage qui « calcule » ces types. On peut le voir dans la réponse fournie par l'interprète lorsque le code de la fonction rouge lui est fourni.

# let rouge(n) =
    sommet_coeur(n) || sommet_carreau(n) ;;
val rouge : Cartes.numero_tas -> bool = <fun>

Certaines fonctions nécessitent des variables qui leur sont propres pour écrire l'algorithme qui les réalise. Ces variables sont appelées des variables locales.

Exemple 4 :

La fonction factorielle

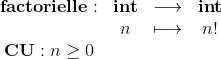
peut s'écrire en Caml

let factorielle(n) =
  let f = ref 1
  in
    for i=1 to n do
      f := !f*i
    done;
    !f

On voit par l'utilisation de la forme let … in … l'emploi d'une variable locale pour coder cette fonction.

Une fonction peut utiliser toute variable globale, à condition qu'elle soit déclarée avant la fonction.

Exemple 5 :

Le code

let un = 1
let plus_un(n) =
   n + un

définit une constante entière qui vaut 1 et la fonction

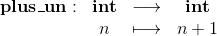
L'expression définissant cette fonction utilise la constante préalablement définie un et se comporte comme on peut s'y attendre.

# plus_un(0);;
- : int = 1

Mais si on redéfinit la constante sans redéfinir la fonction, c'est toujours l'ancienne valeur de la constante qui est prise en compte.

# let un = 2;;
val un : int = 2
# plus_un(0);;
- : int = 1

Comme la fonction superieur, une fonction peut avoir plus d'un paramètre. Ces paramètres peuvent être de types identiques ou non.

Exemple 6 :

La fonction puissance qui à partir de deux entiers a et n renvoie l'entier aⁿ

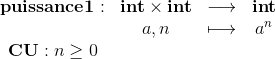
peut s'écrire en Caml avec le code

let puissance1(a,n) =
  let p=ref 1
  in
    for i=1 to n do
      p := !p*a
    done;
    !p

Exemple 7 :

Reprenons la fonction puissance pour des nombres réels.

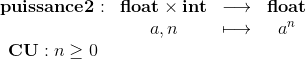
Elle peut s'écrire en Caml avec le code

let puissance2(a,n) =
  let p=ref 1.
  in
    for i=1 to n do
      p := !p*.a
    done;
    !p

Un appel à une fonction à plusieurs paramètres doit se faire avec le bon nombre et le bon type des paramètres. Ainsi, dans l'exemple

# puissance1(2,10);;
- : int = 1024
# puissance2(2.,10);;
- : float = 1024.

les deux appels de fonction sont corrects car effectués avec le bon nombre et les bons types de paramètres. Mais dans l'exemple

# puissance1(2);;
This expression has type int but is here used with type int * int

l'interprète signale une erreur dans l'appel à la fonction puissance1 parce qu'un seul entier a été passé en paramètre au lieu des deux attendus, et dans l'exemple

# puissance2(2,10);;
This expression has type int * int but is here used with type float * int

il signale une erreur parce qu'au lieu du couple (réel, entier) attendu par la fonction puissance2, un couple (entier, entier) lui a été passé.

Il est possible de définir des fonctions sans paramètre. Le type de départ est alors le type unit.

Exemple 8 :

C'est le cas de la procédure prédéfinie print_newline.

Exemple 9 :

La fonction sans paramètre constante égale à 1

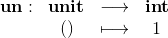
se code en Caml

let un() = 1

et tout appel à cette fonction produit l'entier 1.

# un();;
- : int = 1

On peut réaliser des fonctions sans paramètre non constantes.

Exemple 10 :

Comme son nom l'indique, la fonction

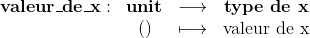
renvoie la valeur de la variable mutable x. En voici le code

let valeur_de_x() = !x

Il est bien entendu préalablement nécessaire d'avoir déclaré une variable mutable x.

# let valeur_de_x() = !x;;
Unbound value x

Si la variable x est déclarée alors le type de la valeur renvoyée par la fonction valeur_de_x est le même que celui de x.

# let x = ref 1;;
val x : int ref = {contents = 1}
# let valeurdex() = !x;;
val valeur_de_x : unit -> int = <fun>
# valeur_de_x();;
- : int = 1
# x := 2;;
- : unit = ()
# valeur_de_x();;
- : int = 2

On peut réaliser des fonctions sans paramètre un peu plus intéressantes.

Exemple 11 :

Supposons que nous voulions programmer une fonction qui simule le lancer d'une pièce de monnaie. Cette fonction doit donner le résultat "PILE" ou "FACE" de manière aléatoire.

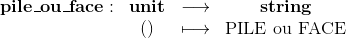
On peut la programmer en utilisant la fonction prédéfinie

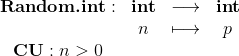
où p est un entier au hasard compris entre 0 inclus et n exclu.

La fonction pile_ou_face se code alors en faisant un appel à Random.int(2) qui produira soit l'entier 0, soit l'entier 1, et en prenant la convention que si c'est 0 alors elle renvoie la valeur "PILE" et si c'est 1 elle renvoie la valeur "FACE".

let pile_ou_face() =
  if Random.int(2) = 0 then
    "PILE"
  else
    "FACE"

Voici une série de quelques appels successifs à cette fonction.

# pile_ou_face();;
- : string = "PILE"
# pile_ou_face();;
- : string = "FACE"
# pile_ou_face();;
- : string = "FACE"
# pile_ou_face();;
- : string = "PILE"

• reflet de l'analyse du problème ;
• modularité ;
• lisibilité des programmes ;
• factorisation du code.

Spécifier une procédure, c'est

• choisir un identificateur pour la nommer ;
• préciser le nombre de paramètres, leur type, et les nommer ;
• indiquer les conditions d'utilisation (CU) que doivent vérifier les paramètres lors d'un appel à la procédure ;
• indiquer l'action de la procédure sur l'environnement (effet de bord).

Par exemple, la procédure du module Cartes permettant de déplacer une carte d'un tas vers un autre se nomme deplacer_sommet. Elle possède deux paramètres de type numero_tas désignant les tas de départ et d'arrivée et possède une contrainte d'utilisation qui est que le tas de départ ne doit pas être vide . Son action modifie les tas de cartes en déplaçant une carte du tas de départ vers le tas d'arrivée. Nous résumons tout cela par la notation :

En Caml, une procédure est une fonction dont le résultat est de type unit. La seule valeur renvoyée par cette fonction est donc l'unique valeur du type unit à savoir (). Les procédures se déclarent donc de la même façon que les fonctions.

Exemple 12 :

let tout_mettre_sur_tas1 () =
  (* vider le tas 2 sur le tas 1 *)
  while tas_non_vide(2) do
    deplacer_sommet(2,1)
  done;
  (* vider le tas 3 sur le tas 1 *)
  while tas_non_vide(3) do
    deplacer_sommet(3,1)
  done;
  (* vider le tas 4 sur le tas 1 *)
  while tas_non_vide(4) do
    deplacer_sommet(4,1)
  done

Exemple 13 :

let vider_tas(depart,arrivee) =
  while tas_non_vide(depart) do
    deplacer_sommet(depart,arrivee)
  done

Cette procédure a pour nom vider_tas et possède deux paramètres (depart et arrivee) qualifiés de formels, car lors de la conception (ou écriture) de cette procédure, ces paramètres n'ont aucune valeur. Ils servent à nommer les (futures) valeurs qui seront passées lors d'un appel à la procédure.

Un appel à une procédure est une instruction. Le résultat de son exécution est une modification de l'état courant de l'environnement ou un affichage de données.

• reflet de l'analyse du problème ;
• modularité ;
• lisibilité des programmes ;
• factorisation du code.

SPECIFIER, SPECIFIER, SPECIFIER

Exercice 6-1

Question 1 : Donnez les spécifications des fonctions et procédures du module Cartes.

Question 2 : Écrivez la fonction sommet_trefle à l'aide de la fonction couleur_sommet.

Exercice 6-2

Réalisez et testez une fonction tas_tous_vides qui renvoie un booléen indiquant si tous les tas sont vides.

Exercice 6-3

Question 1 : Réalisez une fonction tas_max qui donne le numéro du tas dont le sommet a la carte de valeur la plus élevée, parmi les deux tas passés en paramètres. Ne pas oublier les CU.

Question 2 : Réalisez une fonction tas_max3 analogue à la précédente pour trois tas passés en paramètres.

Question 3 : Même chose pour quatre tas ! (paramètres ou non ?)

Exercice 6-4 Ou exclusif

Réalisez une fonction qui renvoie le ou-exclusif des deux booléens passés en paramètres.

Exercice 6-5 Divisibilité

Réalisez le prédicat

Exercice 6-6 Années bissextiles

Une année bissextile est une année qui comprend 366 jours au lieu des 365 pour les années ordinaires.

Depuis l'instauration du calendrier grégorien, sont bissextiles, les années :

• divisibles par 4 mais non divisibles par 100
• ou bien divisibles par 400.

Réalisez la fonction spécifiée ci-dessous

Exercice 6-7 Le plus grand

Question 1 : Réalisez une fonction qui renvoie le plus grand des deux entiers passés en paramètres.

Question 2 : Réalisez de deux façons une fonction qui renvoie le plus grand des trois entiers passés en paramètres

1. en utilisant la fonction définie dans la question précédente ;
2. puis sans utiliser cette fonction.

Exercice 6-8 : Coefficients binomiaux

Étant donnés deux entiers kitxmlcodeinlinelatexdvp0 \le p \le nfinkitxmlcodeinlinelatexdvp, on définit le coefficient binomial par

Réalisez de deux façons la fonction qui à deux entiers associe le coefficient binomial kitxmlcodeinlinelatexdvp\binom{n}{p}finkitxmlcodeinlinelatexdvp

1. une première façon utilisant la fonction factorielle ;

2. une seconde façon exploitant la simplification

   kitxmlcodelatexdvp\binom{n}{p} = \frac{n\times(n-1)\times\dots\times(n-p+1)}{p\times(p-1)\times\dots\times 1}finkitxmlcodelatexdvp

Exercice 6-9 : Fonction polynomiale

Réalisez une fonction qui permet de calculer les valeurs de la fonction réelle de variable réelle

Exercice 6-10 : Plancher et plafond d'un nombre réel

On appelle plancher d'un nombre réel le plus grand nombre entier inférieur ou égal à kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp. On le note kitxmlcodeinlinelatexdvp\lfloor x \rfloorfinkitxmlcodeinlinelatexdvp. Ce nombre est aussi appelé partie entière de kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp.

On appelle plafond d'un nombre réel le plus petit nombre entier supérieur ou égal à kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp. On le note kitxmlcodeinlinelatexdvp\lceil x \rceilfinkitxmlcodeinlinelatexdvp.

Ces deux nombres coïncident lorsque kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp est un nombre entier.

Question 1 : Réalisez une fonction nommée plancher qui calcule le plancher du nombre réel kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp passé en paramètre(13). Il est conseillé de se concentrer d'abord sur le cas des réels positifs ou nuls, puis de généraliser.

Question 2 : De même, réalisez une fonction nommée plafond pour le plafond d'un réel.

Exercice 6-11 Simulation d'un dé

Réalisez une fonction qui simule un dé. Cette fonction renvoie au hasard un entier compris entre 1 et 6.

Exercice 6-12 Tas ordonné ?

Réaliser et tester un prédicat tas1_ordonne qui renvoie vrai si le tas numéro 1 est rangé dans l'ordre croissant. Le tas vide est ordonné, les tas d'une carte le sont aussi. Un tas est ordonné lorsque toute carte du tas est supérieure au sens large à toutes celles qu'elle surmonte. (Comme pour l'exercice précédent plusieurs versions sont possibles.)

Exercice 6-13

Écrire l'entête de la procédure deplacer_sommet du module Cartes. (Le type qui définit les couleurs se nomme couleurs, et celui qui définit les tas se nomme numero_tas.)

Exercice 6-14

Expliquez la condition d'utilisation de la procédure ViderTas.

Exercice 6-15

Question 1 : Reprendre la procédure tout_mettre_sur_tas1 en utilisant la procédure vider_tas (attention à l'ordre des déclarations de ces procédures).

Question 2 : Faire une version paramétrée par le numéro du tas sur lequel on veut tout mettre.

Exercice 6-16 :

Les exercices de manipulation de cartes.

Exercice 6-17 : Tables de multiplication

Spécifiez et réalisez une procédure qui affiche la table de multiplication par un entier donné en paramètre.